Intrinsic Heavy Quark State Contributions

The goal of this project is to find the contributions to partcle yields due to intrinsic quark content of the initial state hadrons. For instance a proton, which consists of a net two up and one down quarks, has some probability of containing a gross of more than three quarks. For instance it may be found to be in the state u u d c c-bar. In this case a D^- (d c-bar) may be diffractively produced at the time of a collision leaving a uuc baryon called an Sigma_c⁺⁺. I only consider production of particles containing heavy quarks because these are the only particles for which pQCD calculations give yield predictions to which my calculations will be small non-perturbative corections to. For now I wll stick to charmed particles.

A list of assumptions made in these calculations

---

My Progress:

In my first calculation I found the momentum distribution of a charm quark in a uudcc-bar state. Here is a plot of the un-normalized results. Next I calculated the momentum distribution of a D^- meson in a uudcc-bar state. Here is a plot of the normalized results which agrees with this solution given to me by Vogt and also with this plot from Brodsky's 1981 Phys Rev D article "Intrinsic Heavy Quark States".

I have come up with a general formula for the momentum distribution of a meson in a hadorn cotaining n particles:

dP_m/dx_mF= 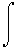...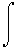x_m (1-x_m)^n-3 R_{i=2 to n-3}(1-x_i)^n-2-i G[x_mx₁, x_m(1-x₁), (1-x_m)x_k-1R_{j=2 to k-1}(1-x_j), (1-x_m)R_{j=2 to n-2}(1-x_j)] R_{s=1 to n}dx_s

Where the limits of integration on all integrals are 0 to 1, x_m is the fraction of the hadron's momentum carried by the meson I am finding the momentum disribution for (ie by the two quarks in the meson), R is the product symbol, The function G[y₁,...,y_n] = (m_h² -sum_{i=1 to n}[m_t²_i/y_i]) ^-2, m_h is the mass of the hadron containing the n partons.

To relate these predictions to experiment I use this relationship to differential cross section

ds/dx=sⁱⁿ(u²/4m_t²_c)*dP/dx

sⁱⁿ is the inelastic hadron nucleon cross section (we assume the target is a nucleon or nucleus), u² is the coherence factor and is estimated to be about 0.1GeV. We use these factors because, since an event with coalescence would be recorded as an inelstic event, the inelastic cross section is the scale at which such events occur and the coherence factor (divided by 4m_t²_c) is the probability that an inelastic event is a coherence event.

I have learned the method of adding the contributions from each of the fock states to the pQCD leading order momentum distribution.

Here is the sum of the intrinsic D^- contributions from all 5, 7 and 9 particle states of the sigma^- summed and weighted by the appropriate factors.

And here is the total D- and D+ distributions for P_beam=600 GeV/c Sigma- on N, with the coalescence and fusion parts summed. Also shown is the fusion and coalescence parts individualy. Clearly the coalescence part is relatively small in the regions where the fusion part is largest. The lower right plot shows that the coalescence part dominates the D- yeild by a factor of 3000 in the region of x=1, but only by a factor of 6 fro the D+. You may note that on the coalescence plot very high x points are at at zero. This is because it is impossable for the D to cary this much of the projectiles momentum. If it did, there would be no energy left over for the mass of the remaining projectile or target!

A leading particle is one containing a quark from the initial state. In some cases is is easy to pick out the leading and non-leading particles, in some cases it is not. For instance if the projectile is a Sigma- and the target is a proton and the final state particles are a Ds-, Sigma c + and neutron than clearly the Ds- is carying the s from the projectile. However, if a pi- is incident on a proton and the final state particles are Ds-, Sigma c 0 and D+ things are not so obvious. So, I adopt the convention that Ds- is leading and Ds+ non-leading in all collisions. similarly, D- and D0bar are called leading,D+ and D0 non-leading. The asymetry between leading and nonleading particles gives us an idea of how the valence quarks in the initial state affect the final state. The asymetry is defined as

A(x)= (ds_l/dx-ds_nl/dx)/(ds_l/dx+ds_nl/dx)

The asymetry between the Ds- and Ds+ particles for the experimental conditions in the SELEX experiment (collisions with carbon and copper targets equiprobable) is seen in this plot. The experimental data from SELEX supports my model. A similar prediction was puiblished in 98 by Vogt and Guttierez.

Here is a plot of the predicted asymetries for all the charmed mesons from Sigma-, Pi- and p on N collisions.
Just to note a few interesting things here:
The Ds from Sigma- on N asymetry goes to 1 at x=1 meaning Ds- and be produced near there but Ds+ can not.
The Ds from p on N asymetry does not go to 1 at high x, this is because of the assumption that each charm hadron that can be produced from a given fock state is eaquaprobable, and the same for each anti-charm particle; since charmed baryons can be produced from the lower fock states but anticharm baryons cannot there are more possable charm particles and thus a given charm particle is less probable than a given anticharm particle. Thus, there is a constant asymetry bewteen the diffractive production parts, but these parts only dominate at high x. So, this constant asymetry should be observed at high x where the diffractive processes dominate and are unnoticable where the fusion contribution dominates at low x. This is the behavior seen in the plot.
The Ds from pi- on N asymetriy is at a constant zero. This is because there are just as many charm particles as anticharm particles that can be diffractively produced from any given fock state of the pion, so the diffractive production contribution to Ds- is the same as the diffractive production contribution to the Ds+, and of course the fusion part is the same, leaving zero asymetry.
The D0 from pi- on N asymetry is not at a flat zero, nor does it approach 1 at high x. This is because of the anti-up quark in the initial state which allows more quark combinations in higher fock states to be c u-bar, thus the D0 is more probable in each fock state, leading to a constant asymetry between the diffractive parts which, again, is not noticed except in the high x region where the diffractive part dominates.
So, the Ds from sigma- case is particularly interesting as two mechanisms are contributing to the asymetry, the initial strangeness content and the smaller probability for charmed particle production. The other asymetries are due to one and or the other of these processes, except for the Ds from pi- on N asymetry.

The asymetry between baryons seems to look a little different. This plot of the lambda asymetry is a good example.

Here, is the asymetry between various barions and their antiparticles from sigma-, pi- and p on N collisions.
And here is the asymetry between the strange baryons and their antiparticles for the same collisions.