Feb 4, 2000

Rutherford Scattering

Roppon Picha and Jiro Oi

Professor Rutledge

Physics 121: Advanced Lab

 

    One performs scattering experiments to study the interactions of particles and atomic natures. Here our goal is to show Rutherford scattering of alpha particles by the atoms in gold foil. We are interested in confirming the Rutherford formula of scattering. Curium (Cm-244, atomic number 96), acting as a radioactive source emitting alpha particles, was enclosed within a protective lead shield. Performed in a vacuum chamber, as to minimize alpha loss by scattering from air molecules, alpha particles ( 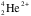) traveling through a hole in the metal shield approach a thin section of gold foil. A gold nucleus (Au-197, atomic number 79), if hit, deflected the alpha particles. From the lab frame, assuming an elastic collision, the alpha particles are observed, using the detector, to head in different angles from their original trajectory. As each alpha particle struck the screen, it would produce a burst of light called a scintillation. The slit chamber is movable, allowing us to determine whether or not any alpha particles were being deflected by the gold foil. Most alpha particles were observed to pass straight through the gold foil, which implied that atoms are composed of large open space. Some alpha particles were deflected slightly, suggesting interactions with other positively charged particles within the atom. Still other alpha particles were scattered at large angles, while a very few even bounced back toward the source. Only a positively charged and relatively heavy particle could account for such strong repulsion. The negative electrons that balanced the nuclear charge were regarded by Rutherford and his colleagues as traveling in circular orbits about the nucleus. By keeping track of the distribution of reflected particles’ locations we can inquire into the nature of atoms. The count rates will determine the differential cross sections at different angles. We make a few graphs to confirm our predictions.

 

Introduction

    Cross section is expressed in terms of area that, if the incident particle hits a circular target of this size perpendicular to its path and centered at a nucleus, the given reaction occurs; and, if it misses the area, the reaction does not occur. In this lab, the equivalence to cross section reaction is the detection of the alpha particle. The results of this study led to the planetary model of the atom, where the nucleus was postulated as small center around which the light, negative electrons circulate at some distance. The scattering of alpha particles from thin gold foil, as observed in the experiments indicates the dense, heavy nature of the nucleus. The electrostatic force of attraction between electrons and nucleus was likened to the gravitational force in the solar system between the planets and the Sun. Most of this planetary atom was open space and offered no resistance to the passage of the alpha particles. The Rutherford model, shown in Fig. 1, based wholly on classical physics, was replaced in a few years by the Bohr atomic model, which incorporated some early quantum theory to better explain the electron orbits.

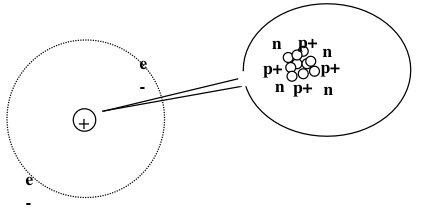
Fig. 1: Rutherford atomic model, proposed that an atom is mostly empty space. There is a small, heavy, positive nucleus with the negative electrons orbiting around the outside edge.

 

Experiments

    Operated in near-vacuum (40-50 milliTorr), the experiment has three major components: the alpha source, the rotating axis, and the detector. The curium source, kept inside the metal packet, radiates alpha particles (the helium nucleus), with approximate energy 6 MeV, as observed on the oscilloscope, through a narrow slit which helps direct the beam to travel in one direction. We study the paths of particles using the detector. Rotating the source enables us to gain the data of counts per minute and different angles. We perform the same process twice, once with nothing between the slit and the detector and the other having the small gold sheet (thickness 0.00025 cm) acting as the screen placed in between. The thickness of the screen is important. It should not be too thin or there would not be enough scattering events, and should not be too thick as that would mean the alpha particles must go through many layers of gold atoms and, as a result, the energy would significantly change. By examining the particle’s path deflected by the Coulomb force 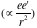, we obtain the Rutherford scattering cross section:

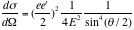
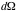     = solid angle element =

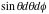
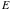     = energy of the alpha particle

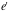     and = the charges of the alpha particle (+2e) and the gold nucleus (+79e).

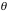     = the scattered angle of the alpha beam.

Therefore we have,

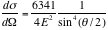. ----- (eq. 1)

    Notice that the cross section changes very rapidly for small angles.

    For the counting process, we must take the background counts -- without the gold foil -- so that we understand the nature of the equipments. From this data, we build the profile of the beam scattered (Fig. 2).

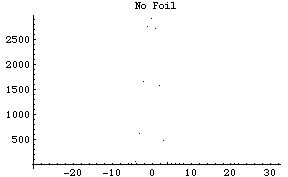
Fig. 2: The distribution of the alpha particles, measured in the vacuum chamber, without the gold foil. (As expected nearly all the particles fall in the very middle. The beam goes straight without deflection.)

 

We find that most particles fall in the range +3 degrees to -3 degrees (Table 1). The peak count rate is 2920 counts/min. Most counts are taken in a span of one minute at each angle, at larger angles (-30, -25, -20, -15, +15, +20, +25, +30), however, we count longer (5 and 10 minutes) as to minimize the error.

    Error = 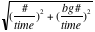; where is total count, time unit is minute.

    Note that these larger angles are adjusted (shifted by 1 degree) by examining the count rate.

    After put in the gold foil, the second beam profile is made. We find that the alpha particles scatter more, most lie in the region -15 degrees to +15 degrees (Fig. 3).

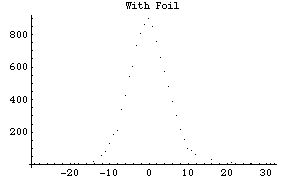
Fig. 3: The distribution of the alpha particles as detected with the gold foil put between the source and the detector. (Most particles still go straight, but there is a significant number of particles deflected. Notice the peak count at 0-degree is around 900, many less compared to around 3000 without the foil.)

 

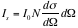
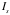     = the number of alpha particles into the detector = R-R’

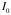     = the total incident beam, measured without the gold sheet

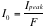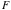     ( = fraction of incident beam)

    

 

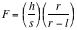
Refer to Fig.4,

 

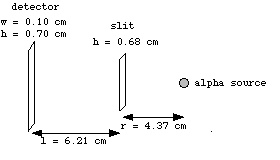
Fig. 4: The equipment setup diagram, showing dimensions of the slit and the detector.

 

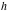     = height of detector = 0.70 cm

     = height of beam slit = 0.68 cm

     = distance from slit to source = 4.37 cm

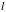     = distance from slit to detector = 6.21 cm

    Therefore, 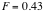, 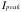= 2920 counts/min --> 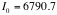counts/min.

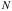= the area density of scatterers =

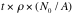
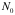     = Avogadro’s number = 6x10 23

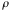     = the density of the foil = 19.3 gr/cm 3

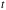     = the thickness of the foil = 0.00025 cm

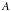     = the atomic weight of gold = 197

So, .

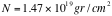The differential cross section is therefore,

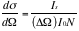
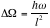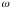; = width of detector = 0.10 cm --> 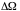= 0.018 sr.

Finally we have,

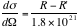. ----- (eq. 2)

Next we try to fit the data, using equations 1 and 2. Applying chi square method over 26 data points,

.

,

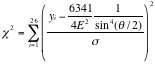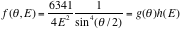
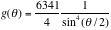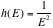
We find that,

.

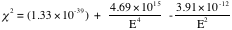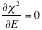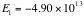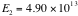--> , ; choose positive energy 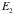. Then we have,

.

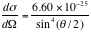Thus,

.

 

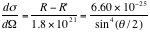Next, we make the log-log plot of 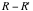and 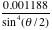to confirm the Rutherford formula. The graph is linear as expected (Fig. 5). The Rutherford scattering cross section relation is confirmed by the experiment.

 

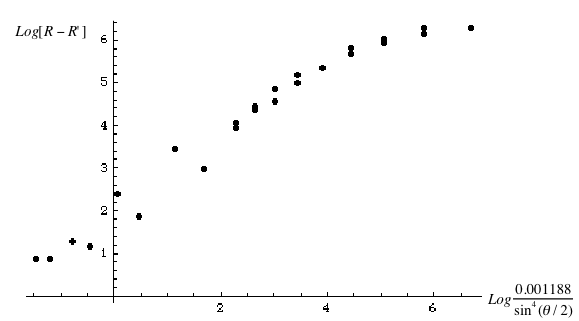
Fig. 5: The Log-Log graph of scattering cross section.

 

 

 

________________________________