Consider the probability distribution
Assume also, for generality, that
Then, the THEOREM says that the cummulative normalized distribution is a uniform distribution:
Fundamental THEOREM for sampling.-
Consider the probability distribution
![]() , i.e.,
, i.e.,
![]() = probability for
= probability for ![]() to be between
to be between ![]() and
and ![]() .
.
Assume also, for generality, that ![]() is limited to the interval (
is limited to the interval (![]() ,
, ![]() ).
).
Then, the THEOREM says that the cummulative normalized distribution is a
uniform distribution:
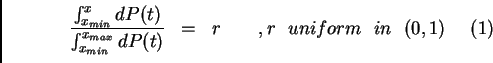
See Figure in Appendix of Green (reference at bottom), which illustrates
the equipartition of areas implict in eq. (1)
We don't prove this result, which for some people can be considered
"manifestly true."
We verify in eq. (1) that for
![]() , and for
, and for
![]() , that is, distribution (1) satisfy the limits corresponding to the
variable
, that is, distribution (1) satisfy the limits corresponding to the
variable ![]() .
.
The THEOREM tell us that the desired value ![]() is obtained by solving
("inverting") eq. (1) for
is obtained by solving
("inverting") eq. (1) for ![]() .
.
A) We next discuss some cases of interest that can be solved
analytically, i.e., ![]() can be expressed explicitily as a function of
can be expressed explicitily as a function of ![]() .
.
1) The distribution is uniform in the interval, for instance, the case of
the azimuthal angle ![]() in scattering.
in scattering.
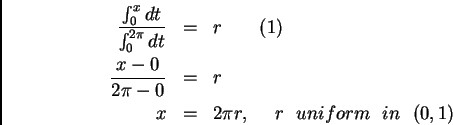
2) Polar angle ![]() for Rutherford scattering for small angles.
for Rutherford scattering for small angles.
![\begin{eqnarray*}
\frac{dP(\theta)} {d\theta} &=& K \frac{1}{\theta^4}, or,...
...ha+1})}]^\frac{1}{\alpha+1}, r uniform in \
(0,1)
\end{eqnarray*}](img14.png)
Note that
a) The multiplicative factor in the distribution is not relevant for the
sampling.
b) For the case ![]() , the distribution reduces to the uniforme
distribution, as it should be.
, the distribution reduces to the uniforme
distribution, as it should be.
3) Mean free path ![]() (or, also, radiactive or particle decay).
These cases correspond to an exponential distribution
(or, also, radiactive or particle decay).
These cases correspond to an exponential distribution
![]() :
:
![\begin{eqnarray*}
\frac{\int_{x_{min}}^x K e^-(t/\Lambda) dt}
{\int_{x_{min}}...
...ac{x_{min}}{\Lambda}})], r uniform in (0,1)
\par\end{eqnarray*}](img18.png)
4) Isotropic angular distribution.-
![]() , that
is, we would like to send, on the average, the same number of particles
into each solid angle .
, that
is, we would like to send, on the average, the same number of particles
into each solid angle .
We have expressed here the element of solid angle ![]() as the product
of two independent variables, each one with a uniform distribution. For
as the product
of two independent variables, each one with a uniform distribution. For
![]() and
and
![]() , we get, from (1):
, we get, from (1):
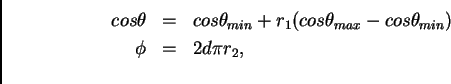
B) If the distribution to be sampled does not have an inverse, that is, if
![]() can not be (easily) expressed as a function of
can not be (easily) expressed as a function of ![]() , it is always possible
to use a method of trial and error that eventually gives us a value of
, it is always possible
to use a method of trial and error that eventually gives us a value of ![]() with the distribution we are looking for. This computational method is
known as the "acceptance/rejection method". See, for instance, the
Appendix to Green or the Particle Data Book.
with the distribution we are looking for. This computational method is
known as the "acceptance/rejection method". See, for instance, the
Appendix to Green or the Particle Data Book.
REFERENCES
Dan Green, "The Physics of Particle Detectors", Cambridge University
Press, 2000. See Appendix K, "Monte Carlo models", p. 348.
Particle Data Group, "Review of Particle Physics", Phys. Rev. D,
66,01001-1 (2002). See "32. Monte Carlo Techniques"