Tres: Multiple scattering y pérdida de energía

5. Scattering elástico electromagnético.-

A.- Colisiones con un núcleo
- Colisiones simples ("single") : Rutherford scattering
- Colisiones multiples (dispersión angular)

B.- Transferencia de energía (importante sólo para los electrones del átomo). Ionización del átomo (liberación de electrones)

5.1 Colisiones simples.- Scattering Coulombiano de partícula con carga $ze$ contra un núcleo de carga atomica $Ze$ a un parámetro de impacto $b$, lo que produce una deflección en ángulo $\theta_R$

Una estimación simple del ángulo de deflección hace uso de la simetría central de la interacción coulombiana y del hecho que la fuerza varía como $1/r^2$. Así, el principal efecto es un cambio en la cantidad de movimiento transversal, $\Delta p_T$:

$$\begin{eqnarray*} \Delta p_T &\sim& F(b) \Delta t \\ F(b) &=& Ze^2/b^2 \\ \De... ...a}{bT} ,\ \ T=energ\'ia \ \ cin\'etica \ \ del \ \ proyectil \\ \end{eqnarray*}$$

5.2 La sección eficaz de scattering de Rutherford.-

$$\begin{eqnarray*} \frac{d\sigma_R}{d\Omega} &=& \frac{b}{sin \theta} \frac{db}{d... ...\frac{1} {{sin}^4(\theta /2)} \ \ (exacta \ \ y \ \ general) \\ \end{eqnarray*}$$

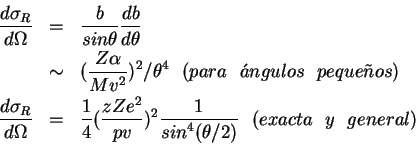
5.4 Consideraciones relativistas.- El campo eléctrico transversal, para un parámetro de impacto dado, aumenta con el factor $\gamma (= \frac{1}{\sqrt{1-\beta^2}})$ (Tabla 3.1 de Green.) Pero el tiempo de colisión decrese por el mismo factor $\gamma$ debido a la dilatación del tiempo. Así, el impulso transversal neto $\Delta p_t$ , y por consiguiente la transferencia de energía, se mantiene constante. Esto corresponde a la llamada zona "de ionización mínima", característica en la detección de partículas ionizantes del altas energías.

5.5 Scattering Coulombiano múltiple.- Notemos primero que hay un ángulo mínimo $\theta_{min}>0$ en el scattering de una partícula. Este ángulo está dado por al tamaño del átomo, es decir, por el radio de Bohr, $a_o$, ya que si el parámetro de impacto $b$ de la partícula incidente excede $\sim a_o$, el campo eléctrico del núcleo que afecta a la partícula se elimina por la presencia de los electrones del átomo ("shielding"). En otras palabras, para $b \sim > a_o$ la carga neta que ve la partícula es 0.

$$\begin{eqnarray*} \theta_{min} &=& b/a_o \\ \theta_{min} &\sim& 2Z\alpha/pva_o \\ \end{eqnarray*}$$

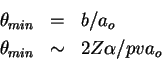
Esto implica que la integral de la sección efficaz diferencial $\textitalic no \ \ diverge$, ya que no hay scattering para $\theta \sim < \theta_{min}$. En otras palabras, para obtener la sección eficaz total de Rutherford, los límites de integración de la sección eficaz diferencial van desde $\theta_{min}$ a $\pi$ en vez de $0$ a $\pi$

Por la relación que hay entre el parámetro de impacto $b$ y el ángulo de scattering $\theta$, que, como vimos, es, para ángulos pequeños, $\theta=2Z\alpha/pvb$, podemos obtener la sección eficaz total de dos formas: a) integrando en el parámetro de impacto y b) integrando en el ángulo:

$$\begin{eqnarray*} a) \ \ \sigma &=& \int_{o}^{a_o} 2\pi b db \\ &\sim& \pi {a_... ...ar\sigma &\sim& \pi {a_o}^2, \ \ tal \ \ como \ \ en \ \ a). \par\end{eqnarray*}$$

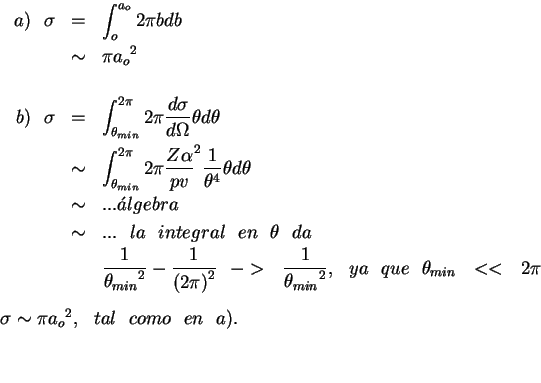
Como se conoce la distribución en los ángulos de scattering, podemos calcular el promedio del ángulo de scattering. Para scattering múltiple, como veremos en seguida, es más conveniente calcular el promedio de $\theta^2$ en vez de $\theta$.

$$\begin{eqnarray*} \overline {\theta^2} &=& \int{\theta^2 \frac{d \sigma}{d \Ome... ...m& 2{\theta_{min}}^2 \ \ ln( \frac{\theta_{min}} {\theta_{max}}) \end{eqnarray*}$$

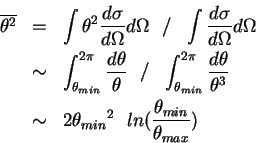
Consideremos enseguida colisiones sucesivas a medida que la partícula cargada atravieza un grosor $dx$ de un material con densidad $rho$ y masa atómica $A$, y que contiene, por consiguiente $N_o \rho dx/A \ \ n\'ucleos \ \ por \ \ {cm}^2$.
En exactamente el mismo razonamiento que en el caso del problema de "random walk" en tres dimensiones, (véase por ejemplo el Reif ("Statistical Physics ...") o, en una forma mas entretenida, G. Gamow, "One, two, ... infinite ...") se puede demostrar que el valor promedio de ${\theta}^2$, si se considera $N$ colisiones elásticas sucesivas está dado por

$$\begin{eqnarray*} \overline {{\theta_{MS}}^2} &=& N \overline {\theta^2}, \ \ c... ...e \ \ \overline L \ \ es \ \ el \ \ camino \ \ medio \ \ libre. \end{eqnarray*}$$

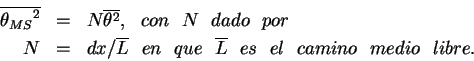
Substituyendo $\frac{1}{\overline L}=N_o\rho\sigma/A$, obtenemos:

$$\begin{eqnarray*} \overline {{\theta_{MS}}^2} &=& \frac{N_o\rho dx}{A} 2 \pi (\frac{2Z\alpha}{p\beta c})^2 \ \ ln(...) \end{eqnarray*}$$

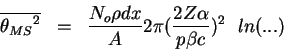
5.6 La longitud de radiación.- Véase Green para una discusión sobre la costumbre en física de altas energías del uso (tradicional) de la longitud de radiación ( el nombre es "desfortunado", ya que no se habla de radiación) para extresar, por ejemplo , $\overline {{\theta_{MS}}^2}$ en función (simple) de esa cantidad.

5.9 Transferencia de energía.- Ya se vió la expresíon para la transferencia de cantidad de movimiemto para scattering coulombiano, de la que se infiere la transferencia de energía cinética:

$$\begin{eqnarray*} \Delta p_T &\sim& 2\alpha/bv \ \ (Z=1)\\ \Delta \epsilon &\si... ...igurosamente, \\ d\epsilon/d\vec{b} &\sim& 2\alpha ^2/(b^2v^2m) \end{eqnarray*}$$

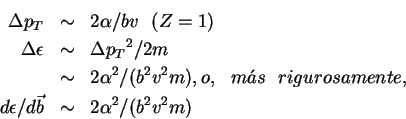
Lo anterior es para una colisión simple con uno de los electrones del átomo a un cierto parámetro de impacto $\vec{b}$. La pérdida de energía promedia (considerando todos los posibles par/'a metros de impacto), será:

$$\begin{eqnarray*} d\epsilon &=& \int_{b_{min}}^{b_{max}} 2\pi b db (d\epsilon/d... ...m& \frac{4\pi {\alpha}^2}{mv^2} \ \ ln (\frac{b_{max}}{b_{min}}) \end{eqnarray*}$$

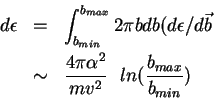
Se observa que la pérdida de energía promedia no depende de la masa, sino sólo de la velocidad y carga del proyectil.

La p'erdida de energía total en el medio es simplemente $d\epsilon \times N$, el número de colisiones que sufre el proyectil al atravezar el medio. Así (el subíndice "1" nos recuerda que esto es para el caso de un proyectil incidente con carga Z=1, proton, por ejemplo):

$$\begin{eqnarray*} \frac{dE_1}{d(\rho x)} &\sim& 4\pi \frac{N_oZ}{A} \alpha^2 \lambda_e/(2\pi)(\frac{1}{\beta^2}) \ \ ln(...) \end{eqnarray*}$$

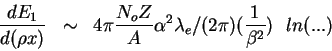
Véase el texto de Hodgson para lo anterior expresado para cualquier proyectil, con una evaluación explícita del término en $ln(..)$.

6.2 Zona de mínima ionización.- Hicimos notar que el campo coulombiano se afecta por el factor $\gamma$,cancelando el correspodiente a la dilatación del tiempo para la partícula incidente, lo que implica una zona en que la transferencia de energía es constante.

6.3 Dependencia en la velocidad.- Rápida variación como $\frac{dE_1}{d(\rho x)} &\sim& \frac{1}{\beta^2} &\sim& \frac{M^2}{p^2}$
A medida que la partícula se frena, pierde más energía (pasa mas tiempo cerca del centro de scattering).

"Máximo" de Bragg, de aplicación, por ejemplo, en el tratamiento del cáncer con haces de iones (protones usualmente).

6.4 Rango.- Integral de la pérdida de energía

6,6 El crecimiento relativista.-