The phi and theta ranges where also divided into 1000 bins and chosen randomly. As each nucleon was generated a check was then run to see if any previously generated nucleons already had this position, if so new phi and theta coordinates where given to the nucleon to preserve the r density distribution. The new coordinates are tested and if they are unique the program moves on.
I have been assured by others who are familiar with MCGlauberModel that the minimum allowed distance between nucleons does not affect the results. I will be testing this myself in the near future. For the record, I am currently using a minimum seperation of .01fm as determined by the number of possable r values (HIJING uses minimum spacing of 0.4fm)
Next, the polar coordinates are converted into rectangular coordinates, and one nucleus is displaced by b along the x axis. A check is run to see if the value (xa-xb)2+(ya-yb)2 is less that sigmaNN/pi between each pair of nucleons. If so, a collision is counted. If at leat one collision is counted for a given nucleon then that nucleon is counted as a participant. Multiple collisions (I call this number nn) are generated for each of many impact paramiters (I call thin sumber nb). The average number of participants from these nn collision is then found and used to calculate
d(sigma)/dNp==
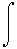P(Np;b)2(pi)b*db where
P(Nch;b)=(2(pi)wNpara2)-.5*exp[-(Npar-Nparave)/(2wNparave)]
As I did for the optical glauber model
My results, don't look right.
the nucleon distributions are to blame.
The problem: by generating random azimuthal angles I am creating a higher density of nucleons at polar angles near zero and pi. A more complicated position generator is needed.
Unfortunately I have run out of time to work on this project. I'd like to thank Dan Cebra for his patience while I put this project together and Ramona Vogt for providing crucial information, as well as Jim Draper for pointing out this last error to me.