Fourire's integral theorem says that if p(x), a complex valued funtion of one real variable, is square integrable (that is, the definite integral of it's modulus squared over all x exists) then

p(x) = (2#)^1/2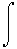_{all k}T(k)e^ikxdk

where
T(k) = (2#)^1/2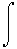_{all x}p(x)e^-ikxdx

this is like having two equations and two unknowns. Combine the expressions.

p(x) = (2#)^1/2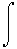_{all k}(2#)^1/2 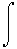_{all x'}p(x')e^-ikx'dx e^ikxdk
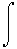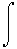= [1/(2#)]_{all k all x'}p(x')e^-ikx'dx e^ikxdk

reversing the order of integration
(There may be some mathematical problem with this)

=[1/(2#)] 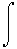_{all x'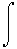all k}p(x')e^-ikx'e^ikxdkdx'
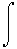= _{all x'}p(x')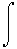_{all k}e^-ik(x-x')dkdx'

checkout the inside integral:

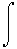_{all k}e^-ik(x-x')dk
When x is not eaqual to x' it gives
lim_{k to infinity}[i/(x-x')] {e^-ik(x-x')-e^ik(x-x')}
= lim_{k to infinity}[2/(x-x')]sin[k(x-x')]